தூண்டலை எவ்வாறு கணக்கிடுவது

இயக்கவியலில் நிறை கொண்ட ஒரு உடல் விண்வெளியில் முடுக்கத்தை எதிர்ப்பது போல, மந்தநிலையை வெளிப்படுத்துகிறது, எனவே மின்கடத்தியில் மின்னோட்டத்தை மாற்றுவதைத் தடுக்கிறது, சுய-தூண்டல் EMF ஐ வெளிப்படுத்துகிறது. இது சுய-தூண்டலின் EMF ஆகும், இது மின்னோட்டத்தின் குறைவு, அதை பராமரிக்க முயற்சிப்பது மற்றும் மின்னோட்டத்தின் அதிகரிப்பு, குறைக்க முயற்சிப்பது ஆகிய இரண்டையும் எதிர்க்கிறது.

உண்மை என்னவென்றால், சுற்றுகளில் மின்னோட்டத்தை மாற்றும் (அதிகரிக்கும் அல்லது குறைக்கும்) செயல்பாட்டில், இந்த மின்னோட்டத்தால் உருவாக்கப்பட்ட காந்தப் பாய்வு மாறுகிறது, இது முக்கியமாக இந்த சுற்று வரையறுக்கப்பட்ட பகுதியில் மொழிபெயர்க்கப்பட்டுள்ளது. காந்தப் பாய்வு அதிகரிக்கும் அல்லது குறையும்போது, ​​அது சுய-தூண்டலின் EMF ஐத் தூண்டுகிறது (லென்ஸின் விதியின்படி - அதை ஏற்படுத்தும் காரணத்திற்கு எதிராக, அதாவது தொடக்கத்தில் குறிப்பிடப்பட்ட மின்னோட்டத்திற்கு எதிராக), அனைத்தும் ஒரே சுற்று. இண்டக்டன்ஸ் L ஆனது தற்போதைய I மற்றும் மொத்த காந்தப் பாய்வு Φ க்கும் இடையே உள்ள விகிதாச்சாரக் காரணி என அழைக்கப்படுகிறது, இந்த மின்னோட்டம் உருவாக்கியது:

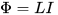
எனவே, சுற்றுவட்டத்தின் தூண்டல் அதிகமாக இருப்பதால், அதன் விளைவாக வரும் காந்தப்புலத்தை விட வலிமையானது, மின்னோட்டத்தை மாற்றுவதைத் தடுக்கிறது (அது அதை உருவாக்கும் புலம்) எனவே மின்னோட்டமானது அதிக தூண்டல் மூலம் மாறுவதற்கு அதிக நேரம் எடுக்கும், அதே மின்னழுத்தத்துடன். பின்வரும் கூற்றும் உண்மைதான்: அதிக தூண்டல், அதன் வழியாக காந்தப் பாய்வு மாறும் போது சுற்று முழுவதும் மின்னழுத்தம் அதிகமாக இருக்கும்.

ஒரு குறிப்பிட்ட பகுதியில் உள்ள காந்தப் பாய்ச்சலை ஒரு நிலையான விகிதத்தில் மாற்றுகிறோம் என்று வைத்துக்கொள்வோம், பின்னர் இந்த பகுதியை வெவ்வேறு சுற்றுகளுடன் மூடுவதன் மூலம், தூண்டல் அதிகமாக உள்ள அந்த சுற்றுக்கு அதிக மின்னழுத்தத்தைப் பெறுவோம் (மின்மாற்றி, ரம்கோர்ஃப் சுருள் போன்றவை இந்த கொள்கையின்படி செயல்படுகின்றன).

ஆனால் லூப் தூண்டல் எவ்வாறு கணக்கிடப்படுகிறது? மின்னோட்டம் மற்றும் காந்தப் பாய்ச்சலுக்கு இடையே உள்ள விகிதாசாரக் காரணியை எவ்வாறு கண்டறிவது? முதலில் நினைவில் கொள்ள வேண்டியது என்னவென்றால், ஹென்ரியில் (எச்) தூண்டல் மாறுகிறது. 1 ஹென்ரி இண்டக்டன்ஸ் கொண்ட சர்க்யூட்டின் டெர்மினல்களில், அதிலுள்ள மின்னோட்டம் நொடிக்கு ஒரு ஆம்பியர் மாறினால், 1 வோல்ட் மின்னழுத்தம் தோன்றும்.

தூண்டலின் அளவு இரண்டு அளவுருக்களைப் பொறுத்தது: சுற்றுகளின் வடிவியல் பரிமாணங்கள் (நீளம், அகலம், திருப்பங்களின் எண்ணிக்கை, முதலியன) மற்றும் நடுத்தரத்தின் காந்த பண்புகள் (எடுத்துக்காட்டாக, உள்ளே ஒரு ஃபெரைட் கோர் இருந்தால். சுருள், அதன் தூண்டல் அதிகமாக இருக்கும், உள்ளே கோர் இல்லை என்றால்).

உற்பத்தி செய்யப்படும் தூண்டலைக் கணக்கிட, சுருள் எந்த வடிவத்தில் இருக்கும் மற்றும் அதன் உள்ளே இருக்கும் ஊடகம் என்ன காந்த ஊடுருவலைக் கொண்டிருக்கும் என்பதை அறிந்து கொள்வது அவசியம் (ஊடகத்தின் ஒப்பீட்டு காந்த ஊடுருவல் என்பது வெற்றிடத்தின் காந்த ஊடுருவலுக்கும் காந்தத்திற்கும் இடையிலான விகிதாசார காரணியாகும். கொடுக்கப்பட்ட ஊடகத்தின் ஊடுருவல்.நிச்சயமாக, இது வெவ்வேறு பொருட்களுக்கு வேறுபட்டது) ...

சுருள்களின் மிகவும் பொதுவான வடிவங்களின் (உருளை சோலனாய்டு, டொராய்டு மற்றும் நீண்ட கம்பி) தூண்டலைக் கணக்கிடுவதற்கான சூத்திரங்களைப் பார்ப்போம்.

தூண்டலைக் கணக்கிடுவதற்கான சூத்திரம் இங்கே சோலனாய்டு - சுருள்கள், அதன் நீளம் விட்டம் விட அதிகமாக உள்ளது:

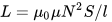
நீங்கள் பார்க்க முடியும் என, திருப்பங்களின் எண்ணிக்கை N, முறுக்கு l இன் நீளம் மற்றும் சுருள் S இன் குறுக்கு வெட்டு பகுதி ஆகியவற்றை அறிந்து, காந்தமாக இருக்கும்போது, ​​​​ஒரு கோர் இல்லாமல் அல்லது ஒரு மையத்துடன் சுருளின் தோராயமான தூண்டலைக் காண்கிறோம். வெற்றிடத்தின் ஊடுருவல் ஒரு நிலையான மதிப்பு:

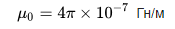
டொராய்டல் சுருளின் தூண்டல், இங்கு h என்பது டொராய்டின் உயரம், r என்பது டொராய்டின் உள் விட்டம், R என்பது டொராய்டின் வெளிப்புற விட்டம்:

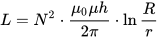
ஒரு மெல்லிய கம்பியின் தூண்டல் (குறுக்குவெட்டின் ஆரம் நீளத்தை விட மிகச் சிறியது), இங்கு l என்பது கம்பியின் நீளம், மற்றும் r என்பது அதன் குறுக்குவெட்டின் ஆரம். I மற்றும் e குறியீடுகளுடன் Mu என்பது உள் (உள், கடத்தி பொருட்கள்) மற்றும் வெளிப்புற (வெளிப்புற, கடத்திக்கு வெளியே உள்ள பொருட்கள்) சூழல்களின் ஒப்பீட்டு காந்த ஊடுருவல்கள்:

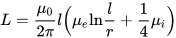
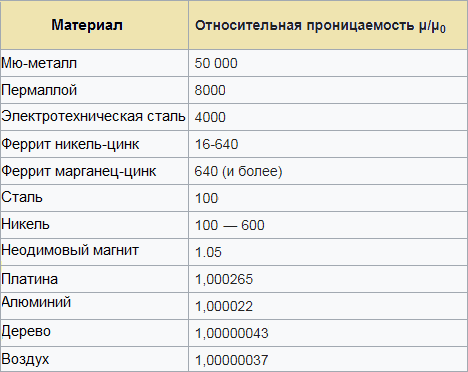
ஒரு குறிப்பிட்ட காந்தப் பொருளை மையமாகப் பயன்படுத்தி ஒரு சுற்று (கம்பி, சுருள்) இலிருந்து நீங்கள் எதிர்பார்க்கக்கூடிய தூண்டலை மதிப்பிடுவதற்கு தொடர்புடைய அனுமதிகளின் அட்டவணை உங்களுக்கு உதவும்: