இழப்புகள் மற்றும் மின்னழுத்த வீழ்ச்சிகள் - வேறுபாடுகள் என்ன

சாதாரண மனித வாழ்க்கையில், "இழப்பு" மற்றும் "வீழ்ச்சி" என்ற சொற்கள் சில சாதனைகளில் குறைவு என்ற உண்மையைக் குறிக்கப் பயன்படுத்தப்படுகின்றன, ஆனால் அவை வேறுபட்ட மதிப்பைக் குறிக்கின்றன.

இந்த வழக்கில், "இழப்புகள்" என்பது ஒரு பகுதியின் இழப்பு, சேதம், முன்னர் அடையப்பட்ட அளவின் அளவைக் குறைத்தல். இழப்புகள் விரும்பத்தகாதவை, ஆனால் அவற்றை நீங்கள் பொறுத்துக்கொள்ளலாம்.

"வீழ்ச்சி" என்ற சொல் உரிமைகளை முழுமையாகப் பறிப்பதோடு தொடர்புடைய மிகவும் கடுமையான தீங்கு என்று புரிந்து கொள்ளப்படுகிறது. இவ்வாறு, எப்போதாவது நிகழும் இழப்புகள் (சொல்லுங்கள், ஒரு போர்ட்ஃபோலியோ) காலப்போக்கில் சரிவுக்கு வழிவகுக்கும் (உதாரணமாக, பொருள் வாழ்க்கையின் நிலை).

இது சம்பந்தமாக, மின் நெட்வொர்க்கின் மின்னழுத்தம் தொடர்பாக இந்த கேள்வியை நாங்கள் கருத்தில் கொள்வோம்.

இழப்புகள் மற்றும் மின்னழுத்த வீழ்ச்சிகள் எவ்வாறு உருவாகின்றன

ஒரு துணை மின்நிலையத்திலிருந்து மற்றொரு துணை மின்நிலையத்திற்கு மேல்நிலைக் கோடுகள் மூலம் மின்சாரம் நீண்ட தூரம் கொண்டு செல்லப்படுகிறது.

மேல்நிலை கோடுகள் அனுமதிக்கப்பட்ட சக்தியை கடத்த வடிவமைக்கப்பட்டுள்ளன மற்றும் ஒரு குறிப்பிட்ட பொருள் மற்றும் பிரிவின் உலோக கம்பிகளால் செய்யப்படுகின்றன. அவை R இன் எதிர்ப்பு மதிப்பு மற்றும் X இன் எதிர்வினை சுமை கொண்ட ஒரு எதிர்ப்பு சுமையை உருவாக்குகின்றன.

பெறும் பக்கத்தில் அது நிற்கிறது மின்மாற்றிமின்சார மாற்றம்.அதன் சுருள்கள் செயலில் மற்றும் உச்சரிக்கப்படும் தூண்டல் எதிர்ப்பு XL ஐக் கொண்டுள்ளன. மின்மாற்றியின் இரண்டாம் பக்கமானது மின்னழுத்தத்தைக் குறைத்து நுகர்வோருக்கு மேலும் கடத்துகிறது, அதன் சுமை Z இன் மதிப்பால் வெளிப்படுத்தப்படுகிறது மற்றும் செயலில், கொள்ளளவு மற்றும் தூண்டல் தன்மை கொண்டது. இது நெட்வொர்க்கின் மின் அளவுருக்களையும் பாதிக்கிறது.

மின் பரிமாற்ற துணை மின்நிலையத்திற்கு மிக அருகில் உள்ள மேல்நிலைக் கோட்டின் ஆதரவின் கம்பிகளுக்குப் பயன்படுத்தப்படும் மின்னழுத்தம், ஒவ்வொரு கட்டத்திலும் சுற்றுகளின் எதிர்வினை மற்றும் செயலில் உள்ள எதிர்ப்பைக் கடந்து, அதில் ஒரு மின்னோட்டத்தை உருவாக்குகிறது, இதன் திசையன் திசையன் திசையிலிருந்து விலகுகிறது. ஒரு கோணம் φ மூலம் மின்னழுத்தம் பயன்படுத்தப்பட்டது.

மின்னழுத்தங்களின் விநியோகத்தின் தன்மை மற்றும் ஒரு சமச்சீர் சுமை பயன்முறைக்கான வரியுடன் மின்னோட்டங்களின் ஓட்டம் புகைப்படத்தில் காட்டப்பட்டுள்ளது.

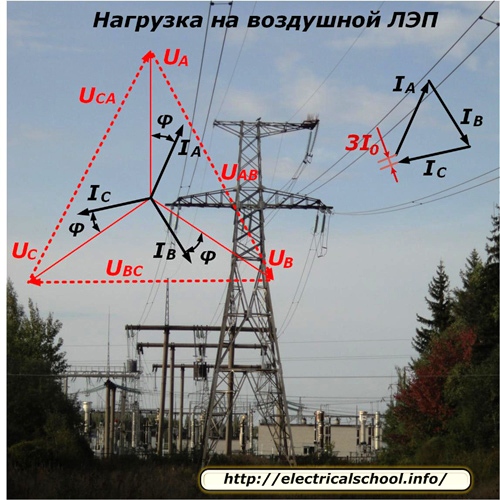
வரிசையின் ஒவ்வொரு கட்டமும் வெவ்வேறு எண்ணிக்கையிலான நுகர்வோருக்கு உணவளிப்பதால், அவர்கள் தற்செயலாக துண்டிக்கப்பட்ட அல்லது வேலையுடன் இணைக்கப்பட்டிருப்பதால், கட்டச் சுமையைச் சரியாகச் சமன் செய்வது தொழில்நுட்ப ரீதியாக மிகவும் கடினம். அதில் எப்போதும் ஒரு ஏற்றத்தாழ்வு உள்ளது, இது கட்ட மின்னோட்டங்களின் திசையன் கூட்டல் மூலம் தீர்மானிக்கப்படுகிறது மற்றும் 3I0 என எழுதப்படுகிறது. பெரும்பாலான கணக்கீடுகளில், இது வெறுமனே புறக்கணிக்கப்படுகிறது.

கடத்தும் துணை மின்நிலையத்தால் நுகரப்படும் ஆற்றல், கோட்டின் எதிர்ப்பைக் கடப்பதில் ஓரளவு செலவிடப்படுகிறது மற்றும் சிறிய மாற்றத்துடன் பெறும் பக்கத்தை அடைகிறது. இந்த பின்னம் இழப்பு மற்றும் மின்னழுத்த வீழ்ச்சியால் வகைப்படுத்தப்படுகிறது, இதன் திசையன் அலைவீச்சில் சிறிது குறைகிறது மற்றும் ஒவ்வொரு கட்டத்திலும் ஒரு கோணத்தால் மாற்றப்படுகிறது.

இழப்புகள் மற்றும் மின்னழுத்த வீழ்ச்சி எவ்வாறு கணக்கிடப்படுகிறது

மின்சாரம் பரிமாற்றத்தின் போது நடைபெறும் செயல்முறைகளைப் புரிந்துகொள்வதற்காக, திசையன் வடிவம் முக்கிய பண்புகளை பிரதிநிதித்துவப்படுத்துவதற்கு வசதியானது. பல்வேறு கணிதக் கணக்கீட்டு முறைகளும் இந்த முறையை அடிப்படையாகக் கொண்டவை.

கணக்கீடுகளை எளிதாக்குவதற்கு மூன்று கட்ட அமைப்பு இது மூன்று ஒற்றை-கட்ட சமமான சுற்றுகளால் குறிக்கப்படுகிறது. இந்த முறை ஒரு சமச்சீர் சுமையுடன் நன்றாக வேலை செய்கிறது மற்றும் அது உடைக்கப்படும் போது செயல்முறைகளை பகுப்பாய்வு செய்ய உங்களை அனுமதிக்கிறது.

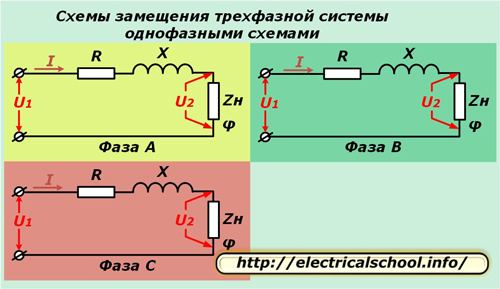
மேலே உள்ள வரைபடங்களில், கோட்டின் ஒவ்வொரு கடத்தியின் செயலில் உள்ள R மற்றும் எதிர்வினை X ஆகியவை φ கோணத்தால் வகைப்படுத்தப்படும் சிக்கலான சுமை எதிர்ப்பு Zn உடன் தொடரில் இணைக்கப்பட்டுள்ளன.

கூடுதலாக, ஒரு கட்டத்தில் மின்னழுத்த இழப்பு மற்றும் மின்னழுத்த வீழ்ச்சியின் கணக்கீடு செய்யப்படுகிறது. இதைச் செய்ய, நீங்கள் தரவைக் குறிப்பிட வேண்டும். இந்த நோக்கத்திற்காக, ஆற்றலைப் பெறும் ஒரு துணைநிலையம் தேர்ந்தெடுக்கப்பட்டது, அங்கு அனுமதிக்கப்பட்ட சுமை ஏற்கனவே தீர்மானிக்கப்பட வேண்டும்.

எந்தவொரு உயர் மின்னழுத்த அமைப்பின் மின்னழுத்த மதிப்பு ஏற்கனவே குறிப்பு புத்தகங்களில் சுட்டிக்காட்டப்பட்டுள்ளது, மேலும் கம்பிகளின் எதிர்ப்புகள் அவற்றின் நீளம், குறுக்குவெட்டு, பொருள் மற்றும் பிணைய கட்டமைப்பு ஆகியவற்றால் தீர்மானிக்கப்படுகின்றன. சுற்றுவட்டத்தில் அதிகபட்ச மின்னோட்டம் அமைக்கப்பட்டு கம்பிகளின் பண்புகளால் வரையறுக்கப்படுகிறது.

எனவே, கணக்கீடுகளைத் தொடங்க, எங்களிடம் உள்ளது: U2, R, X, Z, I, φ.

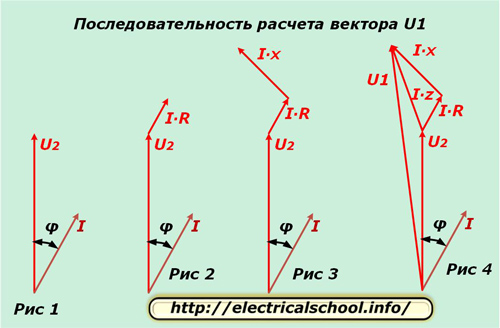
நாம் ஒரு கட்டத்தை எடுத்துக்கொள்கிறோம், எடுத்துக்காட்டாக, «A» மற்றும் சிக்கலான விமானத்தில் U2 மற்றும் I திசையன்கள் பிரிக்கப்படுகின்றன, ஒரு கோணம் φ மூலம் இடம்பெயர்ந்துள்ளது, படம் 1 இல் காட்டப்பட்டுள்ளது. கடத்தியின் செயலில் உள்ள எதிர்ப்பின் சாத்தியமான வேறுபாடு திசையில் ஒத்துப்போகிறது. தற்போதைய மற்றும் அளவுடன் I ∙ R என்ற வெளிப்பாட்டிலிருந்து தீர்மானிக்கப்படுகிறது. U2 (படம் 2) முடிவில் இருந்து இந்த வெக்டரை ஒத்திவைக்கிறோம்.

கடத்தியின் வினைத்திறனில் சாத்தியமான வேறுபாடு ஒரு கோணம் φ1 மூலம் மின்னோட்டத்தின் திசையிலிருந்து வேறுபடுகிறது மற்றும் தயாரிப்பு I ∙ X இலிருந்து கணக்கிடப்படுகிறது. திசையன் I ∙ R (படம் 3) இலிருந்து நாம் அதை ஒத்திவைக்கிறோம்.

நினைவூட்டல்கள்: சிக்கலான விமானத்தில் திசையன்களின் சுழற்சியின் நேர்மறையான திசைக்கு, எதிரெதிர் திசையில் இயக்கம் எடுக்கப்படுகிறது. தூண்டல் சுமை வழியாக பாயும் மின்னோட்டம் பயன்படுத்தப்பட்ட மின்னழுத்தத்தை ஒரு கோணத்தில் பின்தங்குகிறது.

படம் 4 மொத்த கம்பி எதிர்ப்பின் I ∙ Z மற்றும் சுற்று U1 இன் உள்ளீட்டில் உள்ள மின்னழுத்தத்தில் சாத்தியமான வேறுபாடு திசையன்களின் திட்டமிடலைக் காட்டுகிறது.

இப்போது நீங்கள் உள்ளீட்டு திசையன்களை சமமான சுற்று மற்றும் சுமை முழுவதும் ஒப்பிடலாம். இதைச் செய்ய, இதன் விளைவாக வரும் வரைபடத்தை கிடைமட்டமாக வைக்கவும் (படம் 5) மற்றும் திசையன் U2 (படம் 6) இன் திசையுடன் வெட்டும் வரை தொகுதி U1 இன் ஆரம் கொண்ட தொடக்கத்திலிருந்து ஒரு வில் வரையவும்.

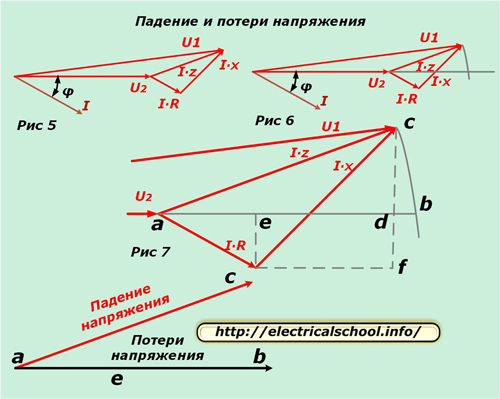
படம் 7 அதிக தெளிவுக்காக முக்கோணத்தின் விரிவாக்கம் மற்றும் துணைக் கோடுகளின் வரைதல் ஆகியவற்றைக் காட்டுகிறது, இது எழுத்துக்களுடன் வெட்டும் சிறப்பியல்பு புள்ளிகளைக் குறிக்கிறது.

இதன் விளைவாக வரும் வெக்டர் ஏசி வோல்டேஜ் டிராப் என்றும், ஏபி லாஸ் என்றும் படத்தின் கீழே காட்டப்பட்டுள்ளது. அவை அளவு மற்றும் திசையில் வேறுபடுகின்றன. நாம் அசல் அளவுகோலுக்குத் திரும்பினால், திசையன்களின் வடிவியல் கழித்தலின் விளைவாக ac பெறப்பட்டதைக் காண்போம் (U2 இலிருந்து U1), மற்றும் ab என்பது எண்கணிதம். இந்த செயல்முறை கீழே உள்ள படத்தில் காட்டப்பட்டுள்ளது (படம் 8).

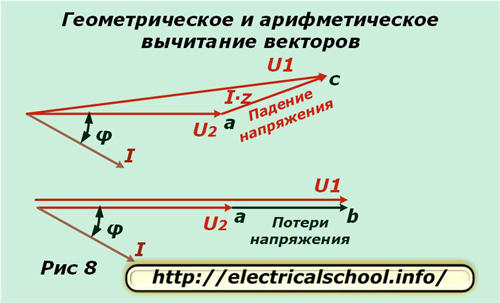
மின்னழுத்த இழப்புகளைக் கணக்கிடுவதற்கான சூத்திரங்களின் வழித்தோன்றல்

இப்போது படம் 7 க்குச் சென்று, bd பிரிவு மிகவும் சிறியதாக இருப்பதைக் கவனியுங்கள். இந்த காரணத்திற்காக, இது கணக்கீடுகளில் புறக்கணிக்கப்படுகிறது மற்றும் மின்னழுத்த இழப்பு பிரிவு நீள விளம்பரத்திலிருந்து கணக்கிடப்படுகிறது. இது Ae மற்றும் ed ஆகிய இரண்டு வரிப் பிரிவுகளைக் கொண்டுள்ளது.

ae = I ∙ R ∙ cosφ மற்றும் ed = I ∙ x ∙ sinφ என்பதால், ஒரு கட்டத்திற்கான மின்னழுத்த இழப்பை சூத்திரம் மூலம் கணக்கிடலாம்:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

அனைத்து கட்டங்களிலும் சுமை சமச்சீராக இருக்கும் என்று நாம் கருதினால் (நிபந்தனையுடன் 3I0 ஐ புறக்கணித்தல்), வரியில் மின்னழுத்த இழப்பைக் கணக்கிட கணித முறைகளைப் பயன்படுத்தலாம்.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

இந்த சூத்திரத்தின் வலது பக்கம் பெருக்கி மற்றும் பிணைய மின்னழுத்தம் Un ஆல் வகுக்கப்பட்டால், மின்சாரம் மூலம் மின்னழுத்த இழப்புகளின் p கணக்கீடு செய்ய அனுமதிக்கும் ஒரு சூத்திரத்தைப் பெறுகிறோம்.

∆Ul = (P ∙ r + Q ∙ x) / Un

செயலில் உள்ள P மற்றும் எதிர்வினை Q சக்தியின் மதிப்புகள் வரி மீட்டர் அளவீடுகளிலிருந்து எடுக்கப்படலாம்.

எனவே, மின்சுற்றில் மின்னழுத்த இழப்பு இதைப் பொறுத்தது:

• சுற்றத்தின் செயலில் மற்றும் எதிர்வினை;

• பயன்படுத்தப்பட்ட சக்தியின் கூறுகள்;

• பயன்படுத்தப்பட்ட மின்னழுத்தத்தின் அளவு.

மின்னழுத்த வீழ்ச்சியின் குறுக்கு கூறுகளைக் கணக்கிடுவதற்கான சூத்திரங்களின் வழித்தோன்றல்

படம் 7 க்கு திரும்புவோம். வெக்டார் ஏசியின் மதிப்பை செங்கோண முக்கோண ஏசிடியின் ஹைப்போடென்யூஸ் மூலம் குறிப்பிடலாம். நாங்கள் ஏற்கனவே விளம்பர பாதத்தை கணக்கிட்டுள்ளோம். குறுக்குவெட்டு கூறு சிடியை தீர்மானிப்போம்.

படம் cd = cf-df என்பதைக் காட்டுகிறது.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

பெறப்பட்ட மாதிரிகளைப் பயன்படுத்தி, சிறிய கணித மாற்றங்களைச் செய்து, மின்னழுத்த வீழ்ச்சியின் குறுக்குக் கூறுகளைப் பெறுகிறோம்.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

மின் வரிசையின் தொடக்கத்தில் மின்னழுத்தம் U1 ஐக் கணக்கிடுவதற்கான சூத்திரத்தை தீர்மானித்தல்

U2 வரியின் முடிவில் உள்ள மின்னழுத்தத்தின் மதிப்பு, இழப்பு ∆Ul மற்றும் துளி δU இன் குறுக்கு கூறு ஆகியவற்றை அறிந்து, பித்தகோரியன் தேற்றம் மூலம் திசையன் U1 இன் மதிப்பைக் கணக்கிடலாம். விரிவாக்கப்பட்ட வடிவத்தில், இது பின்வரும் வடிவத்தைக் கொண்டுள்ளது.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

நடைமுறை பயன்பாடு

மின்னழுத்த இழப்புகளின் கணக்கீடு நெட்வொர்க்கின் உள்ளமைவு மற்றும் அதன் கூறுகளின் உகந்த தேர்வுக்கான மின்சார சுற்று திட்டத்தை உருவாக்கும் கட்டத்தில் பொறியாளர்களால் மேற்கொள்ளப்படுகிறது.

மின் நிறுவல்களின் செயல்பாட்டின் போது, ​​தேவைப்பட்டால், கோடுகளின் முனைகளில் உள்ள மின்னழுத்த திசையன்களின் ஒரே நேரத்தில் அளவீடுகள் அவ்வப்போது மேற்கொள்ளப்படலாம் மற்றும் எளிய கணக்கீடுகளின் முறையால் பெறப்பட்ட முடிவுகளை ஒப்பிடலாம். இந்த முறை அதிகரித்த சாதனங்களுக்கு ஏற்றது. அதிக வேலை துல்லியத்தின் தேவை காரணமாக தேவைகள்.

இரண்டாம் நிலை சுற்றுகளில் மின்னழுத்த இழப்புகள்

ஒரு எடுத்துக்காட்டு மின்னழுத்த மின்மாற்றிகளின் இரண்டாம் நிலை சுற்றுகள் ஆகும், அவை சில நேரங்களில் பல நூறு மீட்டர் நீளத்தை அடைகின்றன மற்றும் அதிகரித்த குறுக்குவெட்டுடன் ஒரு சிறப்பு மின் கேபிள் மூலம் பரவுகின்றன.

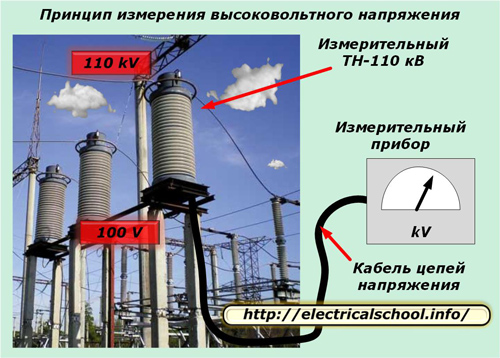
அத்தகைய கேபிளின் மின் பண்புகள் மின்னழுத்த பரிமாற்றத்தின் தரத்திற்கான அதிகரித்த தேவைகளுக்கு உட்பட்டவை.

மின்சார உபகரணங்களின் நவீன பாதுகாப்பிற்கு, உயர் அளவீட்டு குறிகாட்டிகள் மற்றும் 0.5 அல்லது 0.2 என்ற துல்லியமான வகுப்புடன் கூடிய அளவீட்டு அமைப்புகளின் செயல்பாடு தேவைப்படுகிறது. எனவே, அவர்களுக்குப் பயன்படுத்தப்படும் மின்னழுத்தத்தின் இழப்புகள் கண்காணிக்கப்பட்டு கணக்கில் எடுத்துக்கொள்ளப்பட வேண்டும். இல்லையெனில், சாதனங்களின் செயல்பாட்டில் அவர்களால் அறிமுகப்படுத்தப்பட்ட பிழை அனைத்து செயல்பாட்டு பண்புகளையும் கணிசமாக பாதிக்கும்.

நீண்ட கேபிள் வரிகளில் மின்னழுத்த இழப்புகள்

நீண்ட கேபிளின் வடிவமைப்பின் அம்சம் என்னவென்றால், கோர்களை நடத்துவதற்கான மிகவும் நெருக்கமான ஏற்பாடு மற்றும் அவற்றுக்கிடையே ஒரு மெல்லிய அடுக்கு காப்பு ஆகியவற்றின் காரணமாக இது ஒரு கொள்ளளவு எதிர்ப்பைக் கொண்டுள்ளது. இது கேபிள் வழியாக செல்லும் தற்போதைய திசையனை மேலும் திசைதிருப்புகிறது மற்றும் அதன் அளவை மாற்றுகிறது.

I ∙ z இன் மதிப்பை மாற்ற கணக்கீட்டில் கொள்ளளவு எதிர்ப்பின் மீது மின்னழுத்த வீழ்ச்சியின் விளைவை கணக்கில் எடுத்துக்கொள்ள வேண்டும். இல்லையெனில், மேலே விவரிக்கப்பட்ட தொழில்நுட்பம் மாறாது.

மேல்நிலை மின் இணைப்புகள் மற்றும் கேபிள்களில் ஏற்படும் இழப்புகள் மற்றும் மின்னழுத்த வீழ்ச்சிகளின் எடுத்துக்காட்டுகளை கட்டுரை வழங்குகிறது. இருப்பினும், அவை மின்சார மோட்டார்கள், மின்மாற்றிகள், தூண்டிகள், மின்தேக்கி வங்கிகள் மற்றும் பிற சாதனங்கள் உட்பட அனைத்து மின்சார நுகர்வோரிலும் காணப்படுகின்றன.

ஒவ்வொரு வகை மின் உபகரணங்களுக்கும் மின்னழுத்த இழப்புகளின் அளவு இயக்க நிலைமைகளின் அடிப்படையில் சட்டப்பூர்வமாக கட்டுப்படுத்தப்படுகிறது, மேலும் அனைத்து மின்சுற்றுகளிலும் அவற்றின் உறுதிப்பாட்டின் கொள்கை ஒன்றுதான்.