காந்தமோட்ட சக்தி என்றால் என்ன, ஹாப்கின்சன் விதி
19 ஆம் நூற்றாண்டின் இரண்டாம் பாதியில், ஆங்கில இயற்பியலாளர் ஜான் ஹாப்கின்சன் மற்றும் அவரது சகோதரர் எட்வர்ட் ஹாப்கின்சன், காந்த சுற்றுகளின் பொதுவான கோட்பாட்டை உருவாக்கி, "ஹாப்கின்சனின் சூத்திரம்" அல்லது ஹாப்கின்சன் விதி என்று அழைக்கப்படும் ஒரு கணித சூத்திரத்தைப் பெற்றனர், இது ஓம் விதியின் (பயன்படுத்தப்பட்டது) மின்சுற்றுகளை கணக்கிடுவதற்கு).
எனவே, ஓமின் கிளாசிக்கல் விதியானது மின்னோட்டம் மற்றும் மின்னோட்ட விசை (EMF) ஆகியவற்றுக்கு இடையேயான தொடர்பைக் கணித ரீதியாக விவரிக்கிறது என்றால், ஹாப்கின்சன் விதியும் இதேபோல் காந்தப் பாய்ச்சலுக்கும் என்று அழைக்கப்படுவதற்கும் இடையிலான உறவை வெளிப்படுத்துகிறது. காந்தமோட்ட சக்தி (MDF).

இதன் விளைவாக, அது மாறியது காந்தமோட்ட விசை என்பது ஒரு இயற்பியல் அளவு ஆகும், இது காந்தப் பாய்வுகளை உருவாக்கும் மின்சாரத்தின் திறனை வகைப்படுத்துகிறது. இது சம்பந்தமாக ஹாப்கின்சனின் விதி காந்த சுற்றுகளின் கணக்கீடுகளில் வெற்றிகரமாக பயன்படுத்தப்படலாம், ஏனெனில் காந்த சுற்றுகளில் உள்ள MDF ஆனது மின்சார சுற்றுகளில் EMF க்கு ஒத்ததாக உள்ளது. ஹாப்கின்சன் விதி கண்டுபிடிக்கப்பட்ட தேதி 1886 என்று கருதப்படுகிறது.
காந்தமோட்டிவ் விசையின் (எம்.டி.எஃப்) அளவு ஆரம்பத்தில் ஆம்பியர்களில் அளவிடப்படுகிறது அல்லது மின்னோட்டம் அல்லது மின்காந்தத்துடன் கூடிய சுருளைப் பற்றி நாம் பேசினால், கணக்கீடுகளின் வசதிக்காக அதன் வெளிப்பாட்டை ஆம்பியர்-திருப்பங்களில் பயன்படுத்தவும்:
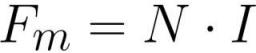
எங்கே: Fm என்பது சுருளில் [ஆம்பியர் * திருப்பம்] காந்தமோட்ட விசை, N என்பது சுருளில் உள்ள திருப்பங்களின் எண்ணிக்கை [திருப்பு], I என்பது சுருளின் [ஆம்பியர்] ஒவ்வொரு திருப்பத்திலும் உள்ள மின்னோட்டத்தின் அளவு.
நீங்கள் இங்கே காந்தப் பாய்வு மதிப்பை உள்ளிட்டால், காந்த சுற்றுக்கான ஹாப்கின்சன் விதி பின்வரும் வடிவத்தை எடுக்கும்:
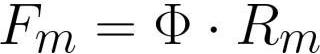
எங்கே: Fm என்பது சுருளில் [ஆம்பியர் * திருப்பம்] உள்ள காந்தமோட்ட விசை, F என்பது காந்தப் பாய்வு [வெபர்] அல்லது [ஹென்ரி * ஆம்பியர்], Rm என்பது காந்தப் பாய்வு கடத்தியின் காந்த எதிர்ப்பு [ஆம்பியர் * திருப்பம் / வெபர்] அல்லது [ முறை / ஹென்ரி] .
ஹாப்கின்சனின் விதியின் உரை உருவாக்கம் முதலில் பின்வருமாறு இருந்தது: "கிளையிடப்படாத காந்த சுற்றுகளில், காந்தப் பாய்வு காந்தமண்டல சக்திக்கு நேர் விகிதாசாரமாகவும் மொத்த காந்த எதிர்ப்பிற்கு நேர்மாறான விகிதாசாரமாகவும் இருக்கும்." அதாவது, இந்தச் சட்டம் சுற்றுவட்டத்தில் உள்ள காந்த சக்தி, தயக்கம் மற்றும் காந்தப் பாய்வு ஆகியவற்றுக்கு இடையேயான உறவை தீர்மானிக்கிறது:
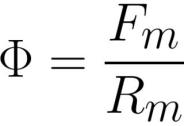
இங்கே: எஃப் என்பது காந்தப் பாய்வு [வெபர்] அல்லது [ஹென்ரி * ஆம்பியர்], Fm என்பது சுருளில் உள்ள காந்தமோட்ட விசை [ஆம்பியர் * புரட்சி], Rm என்பது காந்தப் பாய்வு கடத்தியின் காந்த எதிர்ப்பு [ஆம்பியர் * புரட்சி / வெபர்] அல்லது [ முறை / ஹென்ரி] .
உண்மையில் காந்தமோட்ட விசை (எம்.டி.எஃப்) எலக்ட்ரோமோட்டிவ் ஃபோர்ஸிலிருந்து (ஈ.எம்.எஃப்) ஒரு அடிப்படை வேறுபாட்டைக் கொண்டுள்ளது என்பதைக் கவனத்தில் கொள்ள வேண்டியது அவசியம், இதில் எந்த துகள்களும் நேரடியாக காந்தப் பாய்வில் நகராது, அதே நேரத்தில் மின்னோட்டத்தின் செயல்பாட்டின் கீழ் எழுகிறது. EMF சார்ஜ் செய்யப்பட்ட துகள்களின் இயக்கத்தை எடுத்துக்கொள்கிறது, உதாரணமாக உலோக கம்பிகளில் எலக்ட்ரான்கள். இருப்பினும், MDS இன் யோசனை காந்த சுற்றுகளை கணக்கிடுவதில் உள்ள சிக்கல்களை தீர்க்க உதவுகிறது.
உதாரணமாக, குறுக்கு வெட்டு பகுதி S இன் நுகத்தை உள்ளடக்கிய கிளையில்லாத காந்த சுற்று, அதன் நீளம் முழுவதும் ஒரே மாதிரியாக இருக்கும், மேலும் நுகத்தின் பொருள் காந்த ஊடுருவக்கூடிய mu.
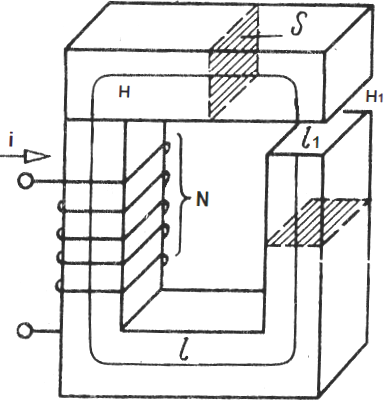
நுகத்தடி இடைவெளி - வெவ்வேறு பொருள், காந்த ஊடுருவல் எந்த mu1. நுகத்தின் மீது வைக்கப்பட்டுள்ள சுருளில் N திருப்பங்கள் உள்ளன, சுருளின் ஒவ்வொரு திருப்பத்திலும் ஒரு மின்னோட்டம் i பாய்கிறது. நுகத்தின் மையக் கோட்டில் காந்தப்புல சுழற்சி தேற்றத்தைப் பயன்படுத்துகிறோம்:
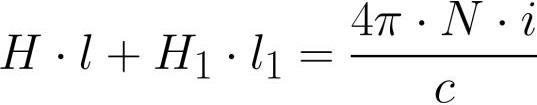
எங்கே: H என்பது நுகத்தின் உள்ளே இருக்கும் காந்தப்புல வலிமை, H1 என்பது இடைவெளிக்குள் இருக்கும் காந்தப்புல வலிமை, l என்பது நுகத்தடி தூண்டலின் மையக் கோடு நீளம் (இடைவெளி இல்லாமல்), l1 என்பது இடைவெளியின் நீளம்.
நுகத்தின் உள்ளேயும் இடைவெளியின் உள்ளேயும் உள்ள காந்தப் பாய்வு ஒரே மதிப்பைக் கொண்டிருப்பதால் (காந்த தூண்டல் கோடுகளின் தொடர்ச்சியின் காரணமாக), Ф = BS மற்றும் В = mu * H என்று எழுதிய பிறகு, காந்தப்புல வலிமையை இன்னும் விரிவாக எழுதுவோம். , மற்றும் இதை மேலே உள்ள சூத்திரத்தில் மாற்றிய பின்:
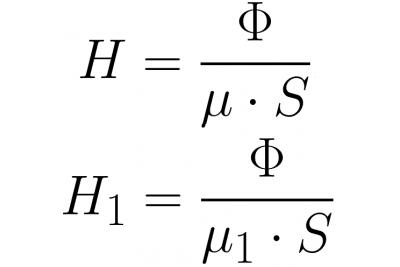
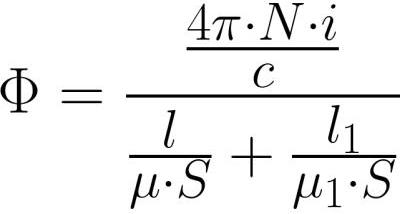
எலக்ட்ரிக்கல் சர்க்யூட்டுகளுக்கான ஓம் விதியில் உள்ள EMF போல, எம்.டி.எஸ்.
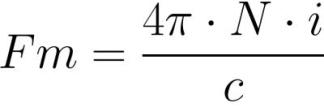
இங்கே எலக்ட்ரோமோட்டிவ் விசை மற்றும் காந்த எதிர்ப்பின் பங்கு வகிக்கிறது
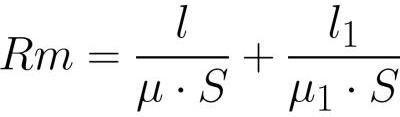
எதிர்ப்பின் பங்கு (ஒப்புமை மூலம் பாரம்பரிய ஓம் விதியுடன்).
