ஒரு ஒற்றை விநியோகத்துடன் பிரிக்கப்படாத மற்றும் கிளைத்த நேரியல் மின்சுற்றுகள்

அதிக எண்ணிக்கையிலான செயலற்ற கூறுகள் இயின் மூலத்துடன் ஒன்றாக இருந்தால். முதலியன c. ஒரு மின்சுற்றை உருவாக்குகிறது, அவற்றின் இணைப்பு வெவ்வேறு வழிகளில் செய்யப்படலாம். அத்தகைய இணைப்புகளுக்கு பின்வரும் பொதுவான திட்டங்கள் உள்ளன.

உறுப்புகளின் தொடர் இணைப்பு இது எளிமையான இணைப்பு. இந்த இணைப்புடன், சுற்றுவட்டத்தின் அனைத்து உறுப்புகளிலும் அதே மின்னோட்டம் பாய்கிறது. இந்த திட்டத்தின் படி, சுற்றுவட்டத்தின் அனைத்து செயலற்ற கூறுகளும் இணைக்கப்படலாம், பின்னர் சுற்று ஒற்றை-சுற்று பிரிக்கப்படாததாக இருக்கும் (படம் 1., a), அல்லது பல-சுற்று சுற்று உறுப்புகளின் ஒரு பகுதி மட்டுமே இருக்க முடியும். இணைக்கப்பட்டுள்ளது.

n உறுப்புகள் தொடரில் இணைக்கப்பட்டிருந்தால், அதே மின்னோட்டம் I பாய்கிறது, சுற்று முனையங்களில் உள்ள மின்னழுத்தம் தொடரில் இணைக்கப்பட்ட n உறுப்புகளில் உள்ள மின்னழுத்த வீழ்ச்சிகளின் கூட்டுத்தொகைக்கு சமமாக இருக்கும், அதாவது.

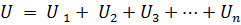
அல்லது:

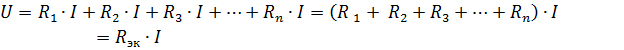
Rek என்பது சமமான சுற்று எதிர்ப்பு.

எனவே, தொடரில் இணைக்கப்பட்ட செயலற்ற உறுப்புகளின் சமமான எதிர்ப்பானது இந்த உறுப்புகளின் எதிர்ப்பின் கூட்டுத்தொகைக்கு சமம்... மின் திட்டம் (படம்.1, a) சமமான மின்சுற்று வழங்கப்படலாம் (படம் 1, b), சமமான எதிர்ப்பு Rek கொண்ட ஒரு உறுப்பு கொண்டது

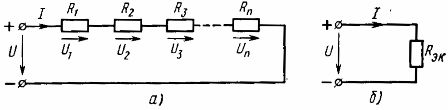
அரிசி. 1. நேரியல் உறுப்புகளின் தொடர் இணைப்பின் திட்டம் (a) மற்றும் அதற்கு சமமான திட்டம் (b)

சக்தி மூலத்தின் கொடுக்கப்பட்ட மின்னழுத்தம் மற்றும் உறுப்புகளின் எதிர்ப்பில் தொடரில் இணைக்கப்பட்ட உறுப்புகளுடன் ஒரு சுற்று கணக்கிடும் போது, ​​சுற்றுவட்டத்தின் மின்னோட்டம் ஓம் விதியின் படி கணக்கிடப்படுகிறது:

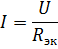
kth உறுப்பு முழுவதும் மின்னழுத்த வீழ்ச்சி

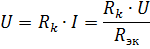
இந்த உறுப்பின் எதிர்ப்பை மட்டுமல்ல, சமமான எதிர்ப்பான ரெக்கையும் சார்ந்துள்ளது, அதாவது சுற்றுவட்டத்தின் மற்ற உறுப்புகளின் எதிர்ப்பையும் சார்ந்துள்ளது. இது உறுப்புகளின் தொடர் இணைப்பின் குறிப்பிடத்தக்க குறைபாடு ஆகும். கட்டுப்படுத்தும் வழக்கில், சுற்றுவட்டத்தின் எந்தவொரு தனிமத்தின் எதிர்ப்பானது முடிவிலிக்கு (திறந்த சுற்று) சமமாக மாறும் போது, ​​சுற்றுவட்டத்தின் அனைத்து உறுப்புகளிலும் உள்ள மின்னோட்டம் பூஜ்ஜியமாக மாறும்.

தொடரில் இணைக்கப்படும்போது, ​​சுற்றுவட்டத்தின் அனைத்து உறுப்புகளிலும் உள்ள மின்னோட்டம் ஒரே மாதிரியாக இருப்பதால், உறுப்புகளில் மின்னழுத்த வீழ்ச்சியின் விகிதம் இந்த உறுப்புகளின் எதிர்ப்பின் விகிதத்திற்கு சமம்:

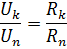
உறுப்புகளின் இணை இணைப்பு - இது ஒரு இணைப்பு ஆகும், இதில் மின்சுற்றின் அனைத்து உறுப்புகளுக்கும் ஒரே மின்னழுத்தம் பயன்படுத்தப்படுகிறது. இணை இணைப்புத் திட்டத்தின் படி, சர்க்யூட்டின் அனைத்து செயலற்ற கூறுகளும் (படம் 2, அ) அல்லது அவற்றின் ஒரு பகுதியை மட்டுமே இணைக்க முடியும். ஒவ்வொரு இணை இணைக்கப்பட்ட உறுப்பு ஒரு தனி கிளையை உருவாக்குகிறது. எனவே, படத்தில் காட்டப்பட்டுள்ள உறுப்புகளின் இணையான இணைப்புடன் கூடிய சுற்று. 2, a, இது ஒரு எளிய சுற்று என்றாலும் (இரண்டு முனைகளை மட்டுமே கொண்டிருப்பதால்), அது அதே நேரத்தில் கிளைத்துள்ளது.

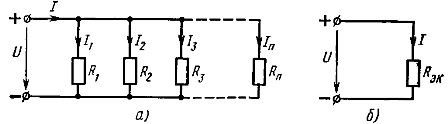
அரிசி. 2. நேரியல் கூறுகளின் இணை இணைப்பு திட்டம் (a) மற்றும் அதற்கு சமமான திட்டம் (b)

ஒவ்வொரு இணை கிளையிலும், மின்னோட்டம்

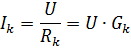
இதில் Gk என்பது kth கிளையின் கடத்துத்திறன் ஆகும்.

இருந்து Kirchhoff இன் முதல் சட்டம்

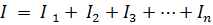
அல்லது

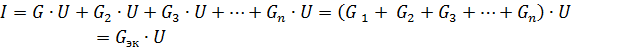
Gec என்பது சமமான சுற்று நடத்துதல் ஆகும்.

எனவே, செயலற்ற கூறுகள் இணையாக இணைக்கப்படும் போது, ​​அவற்றின் சமமான கடத்துத்திறன் இந்த உறுப்புகளின் கடத்துத்திறன்களின் கூட்டுத்தொகைக்கு சமமாக இருக்கும்... இணையான கிளைகளின் எந்தப் பகுதியின் கடத்துத்திறனை விட சமமான கடத்துத்திறன் எப்போதும் அதிகமாக இருக்கும். சமமான கடத்துத்திறன் GEK சமமான எதிர்ப்பு Rek = 1 / Gek உடன் ஒத்துள்ளது.

பின்னர் படத்தில் காட்டப்பட்டுள்ள சமமான சுற்று. 2, a, படத்தில் காட்டப்பட்டுள்ள படிவத்தைக் கொண்டிருக்கும். 2, b. உறுப்புகளின் இணையான இணைப்புடன் சுற்றுவட்டத்தின் பிரிக்கப்படாத பகுதியில் உள்ள மின்னோட்டத்தை ஓம் விதியின்படி இந்த சுற்றுவட்டத்திலிருந்து தீர்மானிக்க முடியும்:

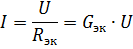
எனவே, விநியோக மின்னழுத்தம் நிலையானதாக இருந்தால், இணையாக இணைக்கப்பட்ட உறுப்புகளின் எண்ணிக்கையில் அதிகரிப்புடன் (இது சமமான கடத்துத்திறன் அதிகரிப்புக்கு வழிவகுக்கிறது), மின்சுற்றின் பிரிக்கப்படாத பகுதியில் (மின்சாரம் தற்போதைய) மின்னோட்டம் அதிகரிக்கிறது.

சூத்திரத்தில் இருந்து

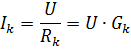
ஒவ்வொரு கிளையிலும் உள்ள மின்னோட்டம் அந்த கிளையின் கடத்துத்திறனை மட்டுமே சார்ந்துள்ளது மற்றும் மற்ற கிளைகளின் கடத்துத்திறன் சார்ந்து இல்லை என்பதைக் காணலாம். ஒருவருக்கொருவர் இணையான கிளை முறைகளின் சுதந்திரம் செயலற்ற கூறுகளின் இணையான இணைப்பின் ஒரு முக்கிய நன்மையாகும். தொழில்துறை நிறுவல்களில், மின் பெறுதல்களின் இணை இணைப்பு பெரும்பாலான சந்தர்ப்பங்களில் பயன்படுத்தப்படுகிறது. மிகவும் தெளிவான உதாரணம் விளக்குகளுக்கு மின்சார விளக்குகளைச் சேர்ப்பதாகும்.

ஒரு இணையான இணைப்பில் அனைத்து உறுப்புகளுக்கும் ஒரே மின்னழுத்தம் பயன்படுத்தப்படுவதால், ஒவ்வொரு கிளையிலும் உள்ள மின்னோட்டம் அந்தக் கிளையின் கடத்துத்திறனுக்கு விகிதாசாரமாக இருப்பதால், இணையான கிளைகளில் உள்ள மின்னோட்டங்களின் விகிதம் இந்த கிளைகளின் கடத்தல்களின் விகிதத்திற்கு சமம் அல்லது நேர்மாறான விகிதாசாரமாகும். அவற்றின் எதிர்ப்பின் விகிதத்திற்கு:

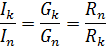
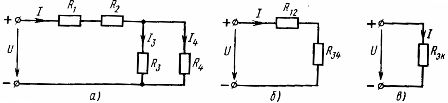
உறுப்புகளின் கலப்பு இணைப்பு என்பது தொடர் மற்றும் இணை இணைப்புகளின் கலவையாகும். அத்தகைய சங்கிலி வெவ்வேறு எண்ணிக்கையிலான முனைகள் மற்றும் கிளைகளைக் கொண்டிருக்கலாம். ஒரு கலப்பு இணைப்பின் உதாரணம் வரைபடத்தில் காட்டப்பட்டுள்ளது (படம் 3, a)

அரிசி. 3. நேரியல் கூறுகள் (a) மற்றும் அதன் சமமான திட்டங்கள் (b, c) ஆகியவற்றின் கலப்பு இணைப்பின் திட்டம்.

அத்தகைய சுற்றைக் கணக்கிடுவதற்கு, தொடர் அல்லது இணையான இணைப்பு மட்டுமே இருக்கும் சுற்றுகளின் பகுதிகளுக்கு சமமான எதிர்ப்பை அடுத்தடுத்து தீர்மானிக்க வேண்டியது அவசியம். கருதப்படும் சுற்றுகளில், R1 மற்றும் R2 எதிர்ப்பைக் கொண்ட உறுப்புகளின் தொடர் இணைப்பு மற்றும் R3 மற்றும் R4 எதிர்ப்புகளுடன் உறுப்புகளின் இணை இணைப்பு உள்ளது. அவற்றின் தொடர் மற்றும் இணையான இணைப்புடன் சுற்று உறுப்புகளின் அளவுருக்களுக்கு இடையில் முன்னர் பெறப்பட்ட உறவுகளைப் பயன்படுத்தி, உண்மையான மின்சுற்று சமமான சுற்றுகளால் அடுத்தடுத்து மாற்றப்படும்.

தொடரில் இணைக்கப்பட்ட உறுப்புகளின் சமமான எதிர்ப்பு

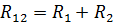
இணையான இணைக்கப்பட்ட உறுப்புகள் R3 மற்றும் R4 ஆகியவற்றின் சமமான எதிர்ப்பு

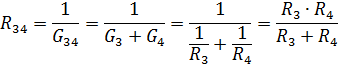
R12 மற்றும் R34 உறுப்புகளின் எதிர்ப்பைக் கொண்ட ஒரு சமமான சுற்று படம் காட்டப்பட்டுள்ளது. 3, பி. R12 மற்றும் R34 இன் இந்தத் தொடர் இணைப்புக்கு, சமமான எதிர்ப்பு

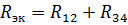
மற்றும் தொடர்புடைய சமமான சுற்று படம் காட்டப்பட்டுள்ளது. 2, பி. இந்த சுற்றுவட்டத்தில் மின்னோட்டத்தைக் கண்டுபிடிப்போம்:

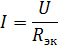
இவை உண்மையான மின்சுற்றின் R1 மற்றும் R2 உறுப்புகளில் வழங்கல் மின்னோட்டம் மற்றும் மின்னோட்டமாகும்.மின்னோட்டங்கள் I3 மற்றும் I4 ஐக் கணக்கிட, மின்சுற்றின் பிரிவில் மின்னழுத்தத்தை R34 எதிர்ப்புடன் தீர்மானிக்கவும் (படம் 3, b):

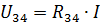
பின்னர் I3 மற்றும் I4 மின்னோட்டங்களை ஓம் விதியின்படி காணலாம்:

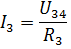
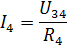
இதேபோல், செயலற்ற கூறுகளின் கலப்பு இணைப்புடன் பல மின்சுற்றுகளை நீங்கள் கணக்கிடலாம்.

அதிக எண்ணிக்கையிலான சுற்றுகள் மற்றும் மின் ஆதாரங்களைக் கொண்ட சிக்கலான சுற்றுகளுக்கு. முதலியன c. அத்தகைய சமமான மாற்றத்தை எப்போதும் மேற்கொள்ள முடியாது. அவை மற்ற முறைகளால் கணக்கிடப்படுகின்றன.