சர்க்யூட் டோபாலஜிஸ்-அடிப்படை கருத்துக்கள்

மின்சுற்று என்பது சாதனங்கள் (உறுப்புகள்) மற்றும் அவற்றின் இணைக்கும் கம்பிகளின் தொகுப்பாகும், இதன் மூலம் மின்சாரம் பாயும். மின்சார சுற்றுகளின் அனைத்து கூறுகளும் பகிர்ந்து கொள்கின்றன செயலற்ற மற்றும் செயலில்.

செயலில் உள்ள கூறுகள் பல்வேறு வகையான ஆற்றலை (இயந்திர, இரசாயன, ஒளி, முதலியன) மின் ஆற்றலாக மாற்றுகின்றன. செயலற்ற சாதனங்களில், மின் ஆற்றல் மற்ற வகை ஆற்றலாக மாற்றப்படுகிறது. செயலில் உள்ள கூறுகள் மூலங்கள் என்று அழைக்கப்படுகின்றன, செயலற்றவை நுகர்வோர் அல்லது பெறுநர்கள் என்று அழைக்கப்படுகின்றன.

சுற்று கோட்பாட்டில், மின் கூறுகளின் சிறந்த மாதிரிகள் கருதப்படுகின்றன. இது உறுப்புகளின் விளக்கத்தை முடிந்தவரை எளிமையாக்குகிறது. மிகவும் சிக்கலான, உண்மையான கூறுகள் இலட்சியப்படுத்தப்பட்ட கூறுகளின் தொகுப்பிலிருந்து வடிவமைக்கப்பட்டுள்ளன.

மின்சுற்றுகளின் முக்கிய செயலற்ற கூறுகள் மின்தடை (எதிர்ப்பு உறுப்பு), தூண்டல் (தூண்டல் உறுப்பு) மற்றும் மின்தேக்கி (கொள்ளளவு உறுப்பு). கொடுக்கப்பட்ட மதிப்பு மற்றும் வடிவத்தின் மின்னழுத்தம் மற்றும் மின்னோட்டத்தை உருவாக்க மின்சுற்றில் கூறுகள் நிறுவப்பட்டுள்ளன (பார்க்க - மின்சார சுற்று மற்றும் அதன் கூறுகள்).

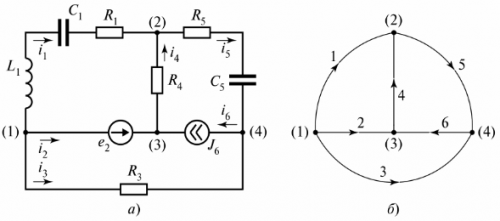
ஒரு மின்சுற்று கிளைகள் மற்றும் முனைகளைக் கொண்டுள்ளது. கிளை - இது ஒரு மின்சுற்றின் (சுற்று) ஒரு பகுதி, இதன் மூலம் அதே மின்னோட்டம் பாய்கிறது. ஒரு முடிச்சு - மூன்று அல்லது அதற்கு மேற்பட்ட கிளைகளின் இணைப்பு. மின் வரைபடத்தில், முனை ஒரு புள்ளியால் குறிக்கப்படுகிறது (படம் 1).

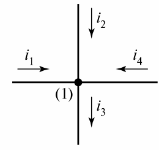
அரிசி. 1. வரைபடத்தில் முனையை வரையறுக்கவும்

தேவைப்பட்டால், வரைபடத்தின் முனைகள் இடமிருந்து வலமாக மேலிருந்து கீழாக எண்ணப்படும்.

அத்திப்பழத்தில். 2 தற்போதைய iC பாயும் மின்தடை-கொள்ளளவு கிளையைக் காட்டுகிறது.

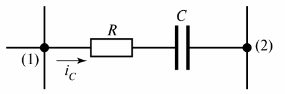
அரிசி. 2. எதிர்ப்பு-கொள்ளளவு கிளை

ஒரு கிளையின் மற்றொரு வரையறை கொடுக்கப்படலாம் - இது இரண்டு அருகில் உள்ள முனைகளுக்கு (படம் 2 இல் உள்ள முனைகள் (1) மற்றும் (2) இடையே உள்ள ஒரு சுற்று ஆகும்.

சங்கிலி மின்சுற்றில் ஏதேனும் மூடிய பாதை உள்ளதா. முடிவிலிக்கு சமமான எதிர்ப்பின் நிபந்தனை கிளைகள் உட்பட எந்த கிளைகளாலும் சுற்று மூடப்படலாம்.

அத்திப்பழத்தில். 3 மூன்று கிளைகளைக் கொண்ட ஒரு கிளை மின்சுற்றைக் காட்டுகிறது.

அரிசி. 3. இரண்டு சுற்றுகள் கொண்ட மின்சுற்று

வரைபடம் மூன்று சுற்றுகளைக் காட்டுகிறது, மேலும் சுற்று I எல்லையற்ற எதிர்ப்பின் கிளையால் மூடப்பட்டுள்ளது. இந்த கிளை மின்னழுத்தம் tiLC என குறிக்கப்படுகிறது.

படம் சுற்றுக்கு. 3 உண்மையான அல்லது நிபந்தனை கிளைகளால் மூடப்பட்ட பல சுழல்களை உருவாக்குவது சாத்தியம், ஆனால் மின் சத்தத்தை கணக்கிடுவதற்கு "சுயாதீன வளையம்" என்ற கருத்து பயன்படுத்தப்படுகிறது. சுயாதீன சுற்று சுழல்களின் எண்ணிக்கை எப்போதும் கணக்கீட்டிற்கு தேவையான குறைந்தபட்சமாக அமைக்கப்படுகிறது.

சுயாதீன சுற்றுகள் எப்போதும் மூடப்பட்டிருக்கும், ஆனால் முடிவிலிக்கு சமமான எதிர்ப்பைக் கொண்ட கிளைகள், மற்றும் ஒவ்வொரு சுயாதீன சுற்று மற்ற சுற்றுகளில் சேர்க்கப்படாத குறைந்தபட்சம் ஒரு கிளையை உள்ளடக்கியது. சிக்கலான மின்சுற்றுகளுக்கு, சுற்று வரைபடத்தைப் பயன்படுத்தி சுயாதீன சுற்றுகளின் எண்ணிக்கையை நீங்கள் தீர்மானிக்கலாம்.

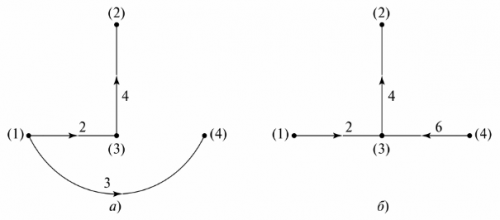
சுற்று வரைபடத்தில் சுற்றுவட்டத்தின் ஒரு நிபந்தனை பிரதிநிதித்துவம் அழைக்கப்படுகிறது, இதில் ஒவ்வொரு கிளையும் ஒரு வரிப் பிரிவால் மாற்றப்படுகிறது. கிளைகளில் உள்ள பொருட்கள் காட்டப்படாது. உதாரணமாக, FIG இல். 4 ஒரு கிளை சுற்று மற்றும் அதன் வரைபடத்தைக் காட்டுகிறது.

அரிசி. 4. கிளை மின்சுற்று: a — சுற்று வரைபடம், b — வரைபடம்

வரைபடத்தின் வரைபடத்தை உருவாக்க, முனைகளில் கூறுகளைக் குறிப்பிடாமல் கிளைக் கோடுகளுடன் இணைக்க வேண்டும். கிளைகள் எண்ணப்பட்டு, அவற்றின் மீது நீரோட்டங்களின் திசைகள் அம்புகளால் குறிக்கப்படுகின்றன. வரைபடத்திற்கு எந்த உடல் அர்த்தமும் இல்லை, ஆனால் சுயாதீனமான வரையறைகளின் எண்ணிக்கை மற்றும் வகையை தீர்மானிக்க பயன்படுத்தலாம். இந்த நோக்கத்திற்காக, ஒரு "கிராஃபிக் மரம்" தயாரிக்கப்படுகிறது.

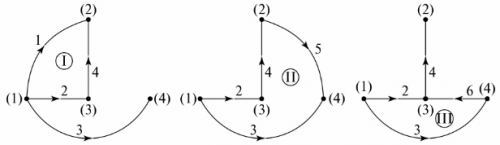
கிராஃபிக் மரம் இது ஒரு சுற்று வரைபடத்தை பிரதிபலிக்கிறது, அதன் முனைகள் கிளைகளால் இணைக்கப்பட்டிருக்கும், எந்த மூடிய வளைய முடிவுகளும் இல்லை. ஒரு வரைகலை மரத்தைக் காண்பிக்க பல விருப்பங்கள் இருக்கலாம். அத்திப்பழத்தில். 5 FIG சுற்றுக்கான இரண்டு சாத்தியமான விருப்பங்களைக் காட்டுகிறது. 4.

அரிசி. 5. திட்டத்தின் கிராஃபிக் மரம்

வரைபட மரத்தில் காணாமல் போன கிளைகளின் எண்ணிக்கை சுற்றுகளின் சுயாதீன சுழல்களின் எண்ணிக்கைக்கு சமம். எடுத்துக்காட்டில், இவை மூன்று கிளைகள், மூன்று சுயாதீன சுழல்கள். வரைபட மரத்தின் முனைகளை வரைபட மரத்தில் குறிப்பிடப்படாத கிளைகளுடன் தொடர்ச்சியாக இணைப்பதன் மூலம் சுயாதீன சுழல்களின் உள்ளமைவைப் பெறலாம். எடுத்துக்காட்டாக, படத்தில் உள்ள வரைபட மரத்திற்கு. 5, மற்றும் சுயாதீனமான வரையறைகள் அத்தியில் காட்டப்பட்டுள்ளன. 6.

அரிசி. 6. வரைபட மரத்தின் மூலம் சுயாதீனமான வரையறைகளை தீர்மானித்தல்

சுற்றைக் கணக்கிடுவதற்கான சுயாதீன சுற்றுகளை உள்ளமைப்பதற்கான விருப்பத்தின் தேர்வு சுற்று பகுப்பாய்வின் போது மேற்கொள்ளப்படுகிறது. அத்தகைய வரையறைகளை நீங்கள் தேர்வு செய்ய வேண்டும், இதனால் கணக்கீடு முடிந்தவரை எளிமையானது, அதாவது. கணினியில் சார்பு சமன்பாடுகளின் எண்ணிக்கை குறைவாக உள்ளது.

இடவியல் சமன்பாடுகள் ஒரு சுற்றுவட்டத்தில் மின்னழுத்தங்கள் மற்றும் நீரோட்டங்களுக்கு இடையே ஒரு உறவை ஏற்படுத்துகின்றன, மேலும் சமன்பாடுகளின் எண்ணிக்கை மற்றும் வகை கிளைகளில் எந்த உறுப்புகள் சேர்க்கப்பட்டுள்ளன என்பதைப் பொறுத்தது அல்ல. இடவியல் சமன்பாடுகளில் இயற்றப்பட்ட சமன்பாடுகள் அடங்கும் Kirchhoff சட்டங்களின்படி.